Modellezés módszertana

ELMÉLET, DEFINÍCIÓK

Potenciális vegetáció

A potenciális természetes vegetáció (Potential Natural Vegetation, PNV) – vagy röviden csak potenciális vegetáció – az a növényzet, amely a jelenlegi élettelen környezet mellett tartósan, emberi behatás nélkül is fenn tud maradni (Tüxen 1956), vagyis a PNV

  • emberi hatások nélkül is életképes növényzeti állapot;
  • fennmaradni képes, tehát nem feltétel, hogy ki is tudjon alakulni az adott körülmények között spontán módon. Ebből következik, hogy sem az adott helyen felhagyás esetén beinduló spontán szukcesszió végállapotával nem kell, hogy azonos legyen, és a szaporítóképletek elérhetősége sem feltétel;
  • jelen időszakra vonatkozik, nem azonos az ember tájátalakító tevékenysége előtti (prehumán) növényzettel. Tüxen eredeti definíciójának bővebb értelmezését és a későbbi értelmezések elemzését lásd Somodi és mtsai. (2012) munkájában.

 Prehumán vegetáció

A prehumán vegetáció az ember tájalakító tevékenységét megelőző növényzet, amely az akkori környezeti viszonyokat tükrözte. Kivételes esetben ezek megegyezhetnek a jelenlegi környezeti viszonyokkal, de a Föld nagy részén az emberi tájátalakító tevékenység olyan régóta folyik, hogy eközben a környezeti viszonyok is megváltoztak. Egyrészt az éghajlat idővel emberi behatás nélkül is változik, illetve tudjuk, hogy változott is. Az éghajlat változása magával vonja a talaj és hosszú távon akár a vízrajz megváltozását is. Másrészt az ember közvetlen módon is alakítja a környezetét, amely különösen a vízkészletek elérhetőségét módosítja, de közvetetten hat az éghajlatra is. Mindezek következtében az egykori és mai környezeti viszonyok eltérnek. De, még ha megegyeznének is, a prehumán vegetáció az akkor megvalósult állapotot jellemzi, aminél az akkori potenciális vegetáció bővebb lehetett. A prehumán vegetációval szemben a potenciális vegetáció modellezése a természetvédelem és a restaurációs ökológia számára hasznosabb információkat nyújthat, hiszen a valaha volt élőhelyek visszaállítása sok esetben már nem reális restaurációs célkitűzés (Jackson és Hobbs 2009).

Többrétegű potenciális természetes vegetáció (MPNV)

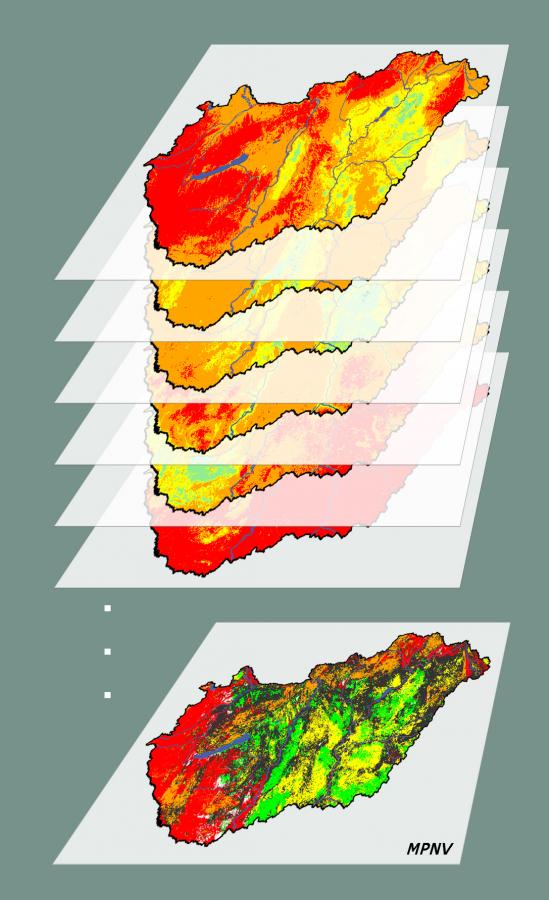Korábbi PNV-modellek, legyenek bár kategorikus (Fischer 1990, Aspinall és Veith 1993, Fischer és mtsai. 2013), szabály alapú (Hemsing és Bryn 2012) vagy a legvalószínűbb élőhelyet kiválasztó (Breziecki és mtsai. 1993, Tichy 1999, Liu és mtsai. 2009) modellezési megközelítések, jellemzően egy földrajzi pontban egy élőhelyet jelöltek meg potenciálisan előforduló típusként. Ugyanakkor a valóságban egy adott helyszínen több különböző élőhely is potenciálisan előfordulhat (ha nem is feltétlenül ugyanakkora valószínűséggel), vagyis egy helynek több PNV-je is lehet – hiszen ugyanazon környezeti viszonyok több élőhely számára is alkalmasak lehetnek. Ezért ha csak egy élőhelyet jelölünk meg mint ott potenciálisan előforduló típust, akkor információt veszítünk. Ezt a megállapítást erősíti, hogy

  • a vegetációtípusok nem feltétlen válnak el élesen átmeneti helyzetben, így az élőhelytípusokat nem is igen tarthatjuk elvágólagos kategóriáknak, inkább elmosódott határú halmazoknak (Roberts 2015);
  • valamint a megfigyelések szerint bolygatatlan környezetben több stabil vegetációs állapot (eltérő élőhely) is ki tud alakulni, vagyis a szukcesszió sztochasztikus (pl. Baker és Walford 1995, Petraitis 2013).

  
Ennek a látszólagos ellentmondásnak a feloldására vezették be Somodi és mtsai. (2012) a többrétegű potenciális természetes vegetáció (Multiple Potential Natural Vegetation, MPNV) fogalmát. Az MPNV képes kezelni a modellezés bizonytalanságát olyan módon, hogy az egyetlen, legvalószínűbb élőhely kiválasztása helyett az összes vizsgált élőhely előfordulási valószínűségét számszerűsíti. Mivel az MPNV-becslések összetettek, ezért számos eltérő lehetőség kínálkozik az eredmények térképes megjelenítésére. Az MPNV ökológiai értelmezéséről és modellezési lehetőségeiről bővebben lásd az e helyütt elérhető becslések tudományos hátterét bemutató szakcikkünket (Somodi és mtsai. 2017).

Kapcsolódó fogalmak

Az előzőekhez kapcsolódó fogalmak még

  • a potenciális, helyszínhez illő vegetáció (Potential Site-adapted Vegetation, PSV, Leuschner, 1997), amely az ember hatására megváltozott környezeti (leginkább vízháztartás- és talaj-) adottságok mellett esetlegesen megtelepedő másodlagos élőhelyeket is figyelembe veszi;
  • valamint a potenciális helyettesítő vegetáció (Potential Replacement Vegetation, PRV), amely feltételezett további antropogén beavatkozások mellett alakulhat ki a területen (Chytrý 1998). Bizonyos értelmezések szerint a PRV az ember segítette inváziós folyamatokat is magában foglalhatja (Chytrý 1998, Somodi és mtsai. 2012);
  • Az előzőekkel rokon fogalom a potenciális jövőbeli természetes vegetáció (Potential Future Natural Vegetation, PFV), amely egy jövőbeli időpontra vonatkoztatott becslés, figyelembe veheti a természetes folyamatok időbeliségét és a bolygatásokat is (Somodi és mtsai. 2012).

  
MODELLEZÉS

Modellezési megközelítés

Magyarországon az emberi tájátalakítás régóta folyik, sok helyütt nincs is írott forrás arról, hogy milyen növényzet volt jelen valaha. Ráadásul részben emberi, részben természetes okokból a mai környezeti háttér már nem feltétlen egyezik meg az átalakított területeken azzal, ami akkor lehetett ott, amikor utoljára természetes növényzet borította. Így aztán mindenképpen valamilyen becslésre kell támaszkodnunk. A becslés alapulhat egy szakértő élete során felgyűlt tapasztalatain, vagy statisztikai összefüggéseken. Az előbbire példa a legelső ilyen becslés Magyarország tekintetében: Zólyomi Bálint potenciális vegetációtérképe (Zólyomi 1967). Ez egy olyan térkép, amelyen a szerző azt próbálta rekonstruálni, hogy az emberi behatások előtt milyen növényzet boríthatta az országot. Potenciális vegetációtérkép ez is, de nem az aktuális környezeti viszonyokat veszi figyelembe. Egy másik példa a szakértői becslésre a MÉTA adatbázisban megtalálható potenciális élőhelyadat, amely a terepi térképező véleményét tükrözi, immár az aktuális környezeti viszonyok mellett (Molnár és mtsai. 2007). A szakértői becslésen alapuló térképek azonban nem terjeszthetők ki sem időben, sem térben, szemben a statisztikai összefüggéseken alapuló becslésekkel, modellekkel.  
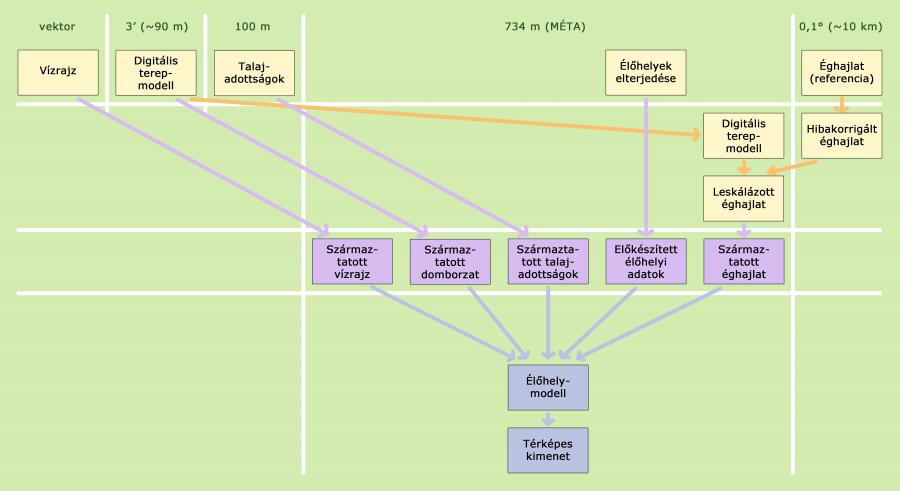
A most közreadott modell alapja a még megmaradt természetes élőhelyek és élettelen környezetük között megfigyelt összefüggések statisztikai formalizálása (a módszertan részletesebb leírását lásd Somodi és mtsai. 2017, valamint Bede-Fazekas 2017 munkájában). Az élőhelyi információkat a MÉTA adatbázisból nyertük, olyan élőhelyeket választottunk, amelyek természetesek és a növényzet természetes fejlődésének (szukcesszió) végső állomásait képviselik. Az élettelen környezetet különböző háttérváltozók jelenítik meg. Ezek jelentős része az éghajlat jellemzője, mint például az éves csapadékösszeg vagy a nyári középhőmérséklet, de a háttérváltozók között domborzati jellemző is szerepel. Emellett figyelembe vettünk talajjellemzőket és a különböző víztestektől (tó, folyó) vett távolságot is.

Modellépítés

Minden vizsgált élőhelyre különálló modellt építettünk, a modellek tanításához az 1977-2006-os referencia-időszakból származó környezeti adatokat használtuk. A modellek építése a predikciótól független, önálló lépés. A lehetséges számos modellezési megközelítés közül választásunk a fejlődő/sokasított regressziós fák (Boosted Regression Trees, BRT, Friedman és mtsai. 2000, Friedman 2002, Schapire 2003) módszerére esett. A BRT prediktív ökológiai modellként való alkalmazása viszonylag újkeletű (De’ath 2007, Elith és mtsai. 2008), ennek ellenére már számos tanulmány rámutatott kiemelkedő prediktív erejére (Elith és mtsai. 2006, Bühlmann és Hothorn 2007, Guisan és mtsai. 2007a). A háttérváltozók közötti magas korreláltság mellett is jól alkalmazható (Bühlmann és Hothorn 2007, Ogutu és mtsai. 2011), amennyiben a korrelációs struktúra a tanító és a predikciós adatbázis között nem tér el lényegesen (Dormann és mtsai. 2013). Kevéssé érzékeny az adatokban lévő hibákra (Graham és mtsai. 2008) és a tanító adatok felbontására (Guisan és mtsai. 2007b).

Predikció, becslés

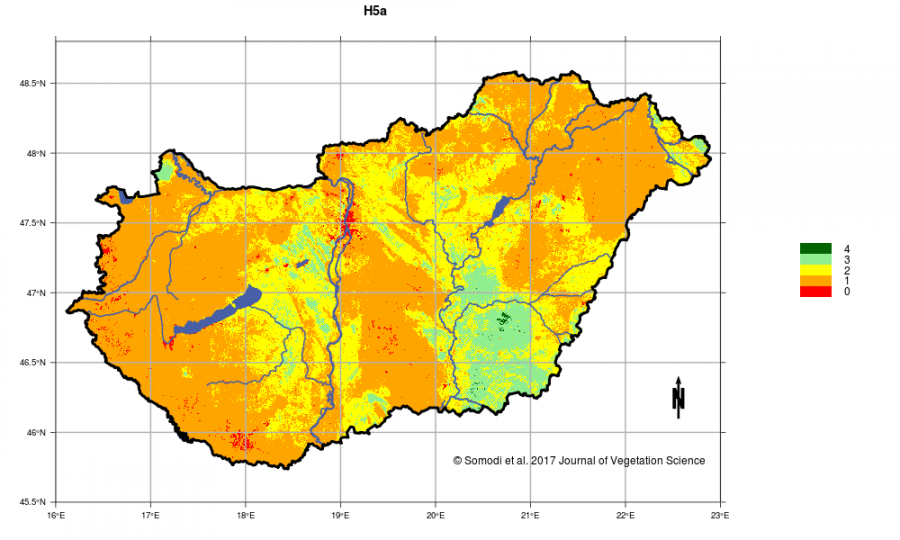A statisztikai modellezés fő eredménye a modellezett élőhelyek lehetséges elterjedésének egy olyan térképsorozata, amely összességében kiadja Magyarország potenciális vegetációtérképét. Egy-egy térkép azt ábrázolja, hogy adott élőhely mekkora valószínűséggel fordulhat elő az ország adott pontján. Ezek alapján megállapíthatjuk, hogy mennyivel lehetne elterjedtebb egy-egy élőhely, hol lehetnének még foltjai, ha az ember nem avatkozna közbe. Ez segítheti a természetvédelmi és élőhely-restaurációs munkák térbeli tervezését azáltal, hogy az élőhely potenciális jelenlétének valószínűsége alapján segít megtalálni a sikerrel leginkább kecsegtető helyszínt. Az egyedi élőhelyek potenciális elterjedését 0 és 1 közötti valószínűségekként tudjuk előállítani. Adott élőhely országon belüli lehetséges elterjedését ezek mutatják a legpontosabban. A nyers valószínűségi értékre igaz, hogy ha az valahol kétszer annyi, akkor ott az élőhelynek kétszer olyan alkalmas a terület. Ezek az értékek azonban élőhelyek között már nem összehasonlíthatóak, mert az egyes élőhelyek abszolút valószínűségi értékei az élőhely jellemzőitől (biológiai és statisztikai, pl. elterjedtség) is függenek. Ezért a valószínűségi értékeket átszámítottuk egy 0-tól 4-ig tartó, ötelemű ordinális skálára, ahol a legmagasabb érték a legnagyobb előfordulási valószínűséget jelenti. Ezeket az értékeket jelenítjük meg a honlapról elérhető térképeken és tesszük elérhetővé a MÉTA adatbázison keresztül. (Egyedi esetben, a szerzőkön keresztül a nyers valószínűségi értékek is kikérhetők.)

HIVATKOZÁS, IRODALMAK

A fenti információk az alábbi publikációból származnak. Részleteket lásd ott:

Hivatkozott irodalmak:

  • Aspinall R, Veitch N (1993): Habitat mapping from satellite imagery and wildlife survey data using a Bayesian modeling procedure in a GIS. Photogrammetric Engineering and Remote Sensing 59: 537–543.
  • Baker WL, Walford GM (1995): Multiple Stable States and Models of Riparian Vegetation Succession on the Animas River, Colorado. Annals of the Association of American Geographers 85: 320–338.
  • Breziecki B, Kienast F, Wildi O (1993): A simulated map of the potential natural forest vegetation of Switzerland. Journal of Vegetation Science 4: 499–508.
  • Bühlmann P, Hothorn T (2007): Boosting algorithms: regularization, prediction and model fitting. Statistical Science 22(4): 477–505.
  • Chytrý M (1998): Potential replacement vegetation: An approach to vegetation mapping of cultural landscapes. Applied Vegetation Science 1(2): 177–188.
  • De’ath G (2007): Boosted trees for ecological modeling and prediction. Ecology 88(1): 243–251.
  • Dormann CF, Elith J, Bacher S, Buchmann C, Carl G, Carré G, García Marquéz JR, Gruber B, Lafourcade B, Leitão PJ, Münkemüller T, McClean C, Osborne PE, Rfeineking B, Schröder B, Skidmore AK, Zurell D, Lautenbach S (2013): Collinearity: a review of methods to deal with it and a simulation study evaluating their performance. Ecography 36(1): 27–46.
  • Elith J, Graham CH, Anderson RP, Dudík M, Ferrier S, Guisan A, Hijmans RJ, Huettmann F, Leathwick JR, Lehmann A, Li J, Lohmann LG, Loiselle BA, Manion G, Moritz C, Nakamura M, Nakazawa Y, Overton JMM, Peterson AT, Phillips SJ, Richardson K, Scachetti-Pereira R, Schapire RE, Soberón J, Williams S, Wisz MS, Zimmermann NE (2006): Novel methods improve prediction of species’ distributions from occurrence data. Ecography 29(2): 129–151.
  • Elith J, Leathwick JR, Hastie T (2008): A working guide to boosted regression trees. Journal of Animal Ecology 77(4): 802–813.
  • Fischer HS (1990): Simulating the distribution of plant communities in an alpine landscape. Coenoses 5: 37–43.
  • Fischer HS, Winter S, Lohberger E, Jehl H, Fischer A (2013): Improving transboundary maps of potential natural vegetation using statistical modeling based on environmental predictors. Folia Geobotanica 48: 115–135.
  • Friedman JH, Hastie T, Tibshirani R (2000): Additive logistic regression: a statistical view of boosting. The Annals of Statistics 28(2): 337–407.
  • Friedman JH (2002): Stochastic gradient boosting. Computational Statistics & Data Analysis 38(4): 367–378.
  • Graham CH, Elith J, Hijmans RJ, Guisan A, Peterson AT, Loiselle BA, NCEAS PSDWG (2008): The influence of spatial errors in species occurrence data used in distribution models. Journal of Applied Ecology 45(1): 239–247.
  • Guisan A, Zimmermann NE, Elith J, Graham CH, Phillips S, Peterson AT (2007): What matters for predicting the occurrences of trees: techniques, data or species’ characteristics? Ecological Monographs 77(4): 615–630.
  • Guisan A, Graham CH, Elith J, Huettmann F, NCEAS SDMG (2007b): Sensitivity of predictive species distribution models to change in grain size. Diversity and Distributions 13(3): 332–340.
  • Hemsing LØ, Bryn A (2012): Three methods for modelling potential natural vegetation (PNV) compared: A methodological case study from south-central Norway. Norsk Geografisk Tidsskrift – Norwegian Journal of Geography 66: 11–29.
  • Jackson ST, Hobbs RJ (2009): Ecological restoration in the light of ecological history. Science  
    325(5940): 567–569.
  • Leuschner C (1997): Das Konzept der potentiellen natürlichen Vegetation (PNV): Schwachstellen und Entwicklungsperspektiven. Flora 192(1): 379–391.
  • Liu H, Wang L, Yang J, Nakagoshi N, Liang C, Wang W, Lv Y (2009): Predictive modeling of the potential natural vegetation pattern in northeast China. Ecological Research 24: 1313–1321.
  • Molnár Zs, Bartha S, Seregélyes T, Illyés E, Botta-Dukát Z, Tímár G, Horváth F, Révész A, Kun A, Bölöni J (2007): A grid-based, satellite-image supported, multi-attributed vegetation mapping method (MÉTA). Folia Geobotanica et Phytotaxonomica 42(3): 225–247.
  • Ogutu JO, Piepho H-P, Schulz-Streeck T (2011): A comparison of random forests, boosting and support vector machines for genomic selection. BMC Proceedings 5(Suppl. 3): S11.
  • Petraitis P (2013): Multiple stable states in natural ecosystems. OUP Oxford.
  • Roberts DW (2015): Potential natural vegetation and environment: a critique of Kusbach, Shaw & Long. Applied Vegetation Science 18: 733–738.
  • Schapire R (2003): The boosting approach to machine learning – an overview. In: Denison DD, Hansen M, Holmes C, Kohn R, Mallick B, Tanner M, Yu B (szerk.): MSRI Workshop on Nonlinear Estimation and Classification. Berkeley, CA, USA: Mathematical Sciences Research Institute.
  • Tichy L (1999): Predictive modeling of the potential natural vegetation in the Podyjí National Park, Czech Republic. Folia Geobotanica 34: 243–252.
  • Tüxen R (1956): Die heutige potentielle natürliche Vegetation als Gegenstand der Vegetationskartierung. Angewandte Pflanzensoziologie (Stolzenau) 13: 4–42.
  • Zólyomi B (1967): Rekonstruált növénytakaró. In: Radó S (szerk.): Magyarország nemzeti atlasza. Budapest: Kartográfiai Vállalat.

 

Kapcsolódó oldalak
Potenciális elterjedési térképek
Felhasználási lehetőségek
Kapcsolódó publikációk
Somodi, Molnár, Czúcz, Bede-Fazekas, Bölöni, Pásztor, Laborczi & Zimmermann (2017)